Silly Spiky Stars And Donuts With OpenGL
Heythere! How’s it going, OpenGL developerpersons? Today I’m going to show you how to draw some slightly more interesting 2D shapes. I won’t be unveiling any fancy new formulas today–just reapplying techniques we’ve already learned in some more interesting ways. Now that you have several of these tutorials under your belt, you should have a pretty good idea how the programs I’ve written are organized. Therefore, I’m going to start writing less English and more JavaScript. I won’t go over each part of the demo in such exhaustive detail as I usually do. Instead, I’ll just provide commentary for the stuff I think is cool and/or new. 🆒🆕
As always, make sure you’ve read the previous tutorials first. Here’s the current list of them:
- Just Draw A Stupid Triangle With OpenGL
- Making A Dopey Circle Thing With OpenGL
- Just Interpolate Already With OpenGL
- Make A Stinking Sprite With OpenGL
- Distorting Sprites’ UV Mappings With OpenGL
Don’t forget that in order to get anything to run on your own computer, you’ll need to have a project folder arranged like we described in the very first tutorial.
I Was Told There’d Be Donuts
Today we’ll be making a spiky star thing, which will remind you a lot of the circle with color interpolation that we did in the third tutorial. It’s pretty much the same thing; its geometry is just a little more advanced. It’s paving the way for even more sophisticated shapes that we could be making down the line.

And yes, I did promise you donuts. So we’ll make one of those too. Its geometry is also a lot like the circle/regular polygons we’ve already made. But instead of a single point at the center, there’s an entire second ring of points that we have to figure out how to link up when we create our Face3s. It’s actually not too bad, but it’s probably more involved than you’d guess if you’d never written an OpenGL program before.
The last step will build upon the uv mapping techniques that we’ve covered in the previous two tutorials. This time I’ll show you how to map a texture onto a mesh that isn’t just a plain old square. The result should be tasty. Take a look!

Code To Copy
Yep. Just copy and paste the whole thing. Put it in the usual opengl_examples directory. We’ll call this file silly_spiky_stars_and_donuts.html.
<!DOCTYPE html>
<html lang="en">
<head>
<title>Silly Spiky Stars And Donuts With OpenGL</title>
<meta charset="utf-8">
<meta name="viewport" content="width=device-width, user-scalable=no, minimum-scale=1.0, maximum-scale=1.0">
<style>
body {
color: #ffffff;
background-color: #000000;
margin: 0px;
overflow: hidden;
}
</style>
</head>
<body>
<div id="container"></div>
<script src="js/three.js"></script>
<script src="js/Detector.js"></script>
<script>
var webGlSupported = Detector.webgl;
if (!webGlSupported) {
Detector.addGetWebGLMessage();
}
var textureLoader = undefined;
var texture = undefined;
var container = undefined;
var camera = undefined;
var scene = undefined;
var renderer = undefined;
initializeTextureLoader();
loadTexture();
function initializeTextureLoader() {
textureLoader = new THREE.TextureLoader();
}
function loadTexture() {
// 1
var url = "images/heres_the_earth.jpg";
var onFinishedLoading = resumeSetup;
var onProgress = function(progressEvent) {};
var onError = function(errorEvent) {console.error("Error loading texture", errorEvent);};
texture = textureLoader.load(url, onFinishedLoading, onProgress, onError);
}
function resumeSetup() {
initializeCamera();
initializeScene();
initializeRenderer();
renderScene();
}
function getStarMaterial() {
return new THREE.MeshBasicMaterial({
vertexColors: THREE.VertexColors,
side: THREE.DoubleSide
});
}
function getDonutMaterial() {
return new THREE.MeshBasicMaterial({
map: texture,
side: THREE.DoubleSide
});
}
// 2
function initializeScene() {
scene = new THREE.Scene();
addStarToScene(-80.0, 0.0);
addDonutToScene(80.0, 0.0);
}
function addMeshToScene(geometry, material, x, y) {
var mesh = new THREE.Mesh(geometry, material);
mesh.position.set(x, y, 0.0);
scene.add(mesh);
}
function addStarToScene(x, y) {
var innerRadius = 25.0;
var outerRadius = 70.0;
var spikesCount = 5;
var geometry = getStarGeometry(innerRadius, outerRadius, spikesCount);
var material = getStarMaterial();
addMeshToScene(geometry, material, x, y);
}
function getStarGeometry(innerRadius, outerRadius, spikesCount) {
var geometry = new THREE.Geometry();
geometry.vertices = getStarVertices(innerRadius, outerRadius, spikesCount);
geometry.faces = getStarFaces(spikesCount);
return geometry;
}
// 3
function getStarVertices(innerRadius, outerRadius, spikesCount) {
var vertices = [];
var centerPoint = new THREE.Vector3(0.0, 0.0, 0.0);
vertices.push(centerPoint);
for (var spikeIndex = 0; spikeIndex < spikesCount; spikeIndex++) {
var spikeProgress = spikeIndex / spikesCount;
var spikePoint = getRadialPoint(spikeProgress, outerRadius);
vertices.push(spikePoint);
var pitProgress = (spikeIndex + 0.5) / spikesCount;
var pitPoint = getRadialPoint(pitProgress, innerRadius);
vertices.push(pitPoint);
}
return vertices;
}
function getStarFaces(spikesCount) {
var faces = [];
var facesCount = spikesCount * 2;
var cyan = new THREE.Color(0.0, 1.0, 1.0);
var purple = new THREE.Color(0.5, 0.0, 1.0);
var vertexColors = [
purple,
cyan,
purple
];
var centerPointIndex = 0;
for (faceIndex = 0; faceIndex < facesCount; faceIndex++) {
var face = new THREE.Face3();
var trailingOuterPointIndex = faceIndex + 1;
var leadingOuterPointIndex = faceIndex + 2;
if (leadingOuterPointIndex > facesCount) {
leadingOuterPointIndex -= facesCount;
}
var normal = undefined;
var face = new THREE.Face3(centerPointIndex, trailingOuterPointIndex, leadingOuterPointIndex, normal, vertexColors);
faces.push(face);
}
return faces;
}
function addDonutToScene(x, y) {
var innerRadius = 10.0;
var outerRadius = 70.0;
var sidesCount = 90;
var geometry = getDonutGeometry(innerRadius, outerRadius, sidesCount);
var material = getDonutMaterial();
addMeshToScene(geometry, material, x, y);
}
function getDonutGeometry(innerRadius, outerRadius, sidesCount) {
var geometry = new THREE.Geometry();
geometry.vertices = getDonutVertices(innerRadius, outerRadius, sidesCount);
geometry.faces = getDonutFaces(sidesCount);
geometry.faceVertexUvs[0] = getDonutFaceUvLayer(sidesCount);
return geometry;
}
// 4
function getDonutVertices(innerRadius, outerRadius, sidesCount) {
var vertices = [];
for (var sideIndex = 0; sideIndex < sidesCount; sideIndex++) {
var sideProgress = sideIndex / sidesCount;
var innerPoint = getRadialPoint(sideProgress, innerRadius);
vertices.push(innerPoint);
var outerPoint = getRadialPoint(sideProgress, outerRadius);
vertices.push(outerPoint);
}
return vertices;
}
// 5
function getDonutFaces(sidesCount) {
var faces = [];
var pointsCountPerSide = 2;
var pointsCount = sidesCount * pointsCountPerSide;
for (var sideIndex = 0; sideIndex < sidesCount; sideIndex++) {
var trailingInnerPointIndex = pointsCountPerSide * sideIndex;
var trailingOuterPointIndex = trailingInnerPointIndex + 1;
var leadingInnerPointIndex = (trailingInnerPointIndex + 2) % pointsCount;
var leadingOuterPointIndex = (trailingInnerPointIndex + 3) % pointsCount;
var trailingFace = new THREE.Face3(
trailingInnerPointIndex,
trailingOuterPointIndex,
leadingInnerPointIndex
);
faces.push(trailingFace);
var leadingFace = new THREE.Face3(
trailingOuterPointIndex,
leadingInnerPointIndex,
leadingOuterPointIndex
);
faces.push(leadingFace);
}
return faces;
}
// 6
function getDonutFaceUvLayer(sidesCount) {
var faceUvLayer = [];
for (var sideIndex = 0; sideIndex < sidesCount; sideIndex++) {
var trailingProgress = sideIndex / sidesCount;
var leadingProgress = (sideIndex + 1) / sidesCount;
var trailingInnerUv = new THREE.Vector3(trailingProgress, 1.0, 0.0);
var trailingOuterUv = new THREE.Vector3(trailingProgress, 0.0, 0.0);
var leadingInnerUv = new THREE.Vector3(leadingProgress, 1.0, 0.0);
var leadingOuterUv = new THREE.Vector3(leadingProgress, 0.0, 0.0);
var trailingUvs = [
trailingInnerUv,
trailingOuterUv,
leadingInnerUv
];
faceUvLayer.push(trailingUvs);
var leadingUvs = [
trailingOuterUv,
leadingInnerUv,
leadingOuterUv
];
faceUvLayer.push(leadingUvs);
}
return faceUvLayer;
}
function getRadialPoint(progress, radius) {
var angle = progress * 2.0 * Math.PI;
var x = Math.cos(angle) * radius;
var y = Math.sin(angle) * radius;
return new THREE.Vector3(x, y, 0.0);
}
function initializeCamera() {
var aspectRatio = window.innerWidth / window.innerHeight;
var screenWidth = undefined;
var screenHeight = undefined;
if (aspectRatio > 1.0) {
screenWidth = 320.0 * aspectRatio;
screenHeight = 320.0;
} else {
screenWidth = 320.0;
screenHeight = 320.0 / aspectRatio;
}
var nearPlane = 1.0;
var farPlane = 1000.0;
camera = new THREE.OrthographicCamera(
-0.5 * screenWidth,
0.5 * screenWidth,
0.5 * screenHeight,
-0.5 * screenHeight,
nearPlane,
farPlane
);
var distanceFromScene = 500.0;
camera.position.set(0.0, 0.0, distanceFromScene);
}
function initializeRenderer() {
renderer = new THREE.WebGLRenderer();
renderer.setPixelRatio(window.devicePixelRatio);
renderer.setSize(window.innerWidth, window.innerHeight);
container = document.getElementById("container");
container.appendChild(renderer.domElement);
}
function renderScene() {
renderer.render(scene, camera);
}
</script>
</body>
</html>
Hokay, So, Here’s The Earth (ROUND)
Before you can run the code, you’ll also need the texture that I’m using for the donut. You can drop it in the images directory along with poop.png and goat.jpg. This one’s called heres_the_earth.jpg. Just look at those cakey icecaps and frosted oceans. Mmm.
(Click the image to download a copy.)
Updating Texture Names
// 1
var url = "images/heres_the_earth.jpg";
Most of the code strongly resembles what we did last time for the goats. In part // 1, all I’m doing is updating the name of the texture that we’re loading. If you don’t do that, you’ll just end up with a donut-shaped goat. Although that is amusing to think about.
Get Situated
I only marked part // 2 to call your attention to the general organization of the program this time around. addStarToScene relies on getStarMaterial and getStarGeometry, which relies on getStarVertices and getStarFaces. The donut’s creation goes through similar methods. Take a minute or two to trace through the flow of the program and make sure it makes sense. There shouldn’t be anything surprising in there.
// 2
function initializeScene() {
scene = new THREE.Scene();
addStarToScene(-80.0, 0.0);
addDonutToScene(80.0, 0.0);
}
Danger: Sharp Objects Ahead
Like I said, part // 3 should remind you a lot of the regular polygons we’ve already created.
// 3
function getStarVertices(innerRadius, outerRadius, spikesCount) {
var vertices = [];
var centerPoint = new THREE.Vector3(0.0, 0.0, 0.0);
vertices.push(centerPoint);
for (var spikeIndex = 0; spikeIndex < spikesCount; spikeIndex++) {
var spikeProgress = spikeIndex / spikesCount;
var spikePoint = getRadialPoint(spikeProgress, outerRadius);
vertices.push(spikePoint);
var pitProgress = (spikeIndex + 0.5) / spikesCount;
var pitPoint = getRadialPoint(pitProgress, innerRadius);
vertices.push(pitPoint);
}
return vertices;
}
Only this time there are spikes. This time we have an outer ring of vertices (the spikePoints) and an interspersed, inner ring of vertices (the pitPoints). With each iteration, we add a spikePoint and a pitPoint to our vertices array. Once we’ve made it all the way around the shape, we return vertices so that we can plug it into our geometry object.
It’s probably worth glancing at getStarFaces right below it too, just to see how I handled having double the number of vertices. The colors are set up slightly differently as well.
That’s really all that goes into making a star mesh! Go ahead and mess around with the parameters defined in addStarToScene. See how high you can crank spikesCount! Maybe rearrange the colors in getStarFaces. Just be careful not to cut yourself on those spikes.
Donuts Donuts Donuts Donuts Donuts!
Okay, okay! Chill out! We’re about to get started on that donut. Check out part // 4.
// 4
function getDonutVertices(innerRadius, outerRadius, sidesCount) {
var vertices = [];
for (var sideIndex = 0; sideIndex < sidesCount; sideIndex++) {
var sideProgress = sideIndex / sidesCount;
var innerPoint = getRadialPoint(sideProgress, innerRadius);
vertices.push(innerPoint);
var outerPoint = getRadialPoint(sideProgress, outerRadius);
vertices.push(outerPoint);
}
return vertices;
}
This method gets called by getDonutGeometry right above. It’s sort of similar to the approach that we used for getStarVertices. The difference here is that both the innerPoint and the outerPoint are positioned at the same sideProgress around the circle. They just have different radius values.
That Was The Easy Part
Now we have to figure out how to connect the points we just plotted with triangles. This is a little trickier than anything we’ve done before. Scroll on down to // 5.
// 5
function getDonutFaces(sidesCount) {
var faces = [];
var pointsCountPerSide = 2;
var pointsCount = sidesCount * pointsCountPerSide;
for (var sideIndex = 0; sideIndex < sidesCount; sideIndex++) {
var trailingInnerPointIndex = pointsCountPerSide * sideIndex;
var trailingOuterPointIndex = trailingInnerPointIndex + 1;
var leadingInnerPointIndex = (trailingInnerPointIndex + 2) % pointsCount;
var leadingOuterPointIndex = (trailingInnerPointIndex + 3) % pointsCount;
var trailingFace = new THREE.Face3(
trailingInnerPointIndex,
trailingOuterPointIndex,
leadingInnerPointIndex
);
faces.push(trailingFace);
var leadingFace = new THREE.Face3(
trailingOuterPointIndex,
leadingInnerPointIndex,
leadingOuterPointIndex
);
faces.push(leadingFace);
}
return faces;
}
We’re using texture mapping this time, so at least we don’t have to worry about colors when we’re building our Face3s. Let’s take a look at a wireframe version of our donut to get a sense of how its triangles are arranged. Here’s a skinnier donut with a sidesCount of 60.

But it’s still kind of hard to follow what’s going on. Let’s chop the sidesCount down to 6.

That’s better. I wonder if you’d call that a hex-nut. Get it? 😜🔩
Sorry. I couldn’t resist. Anyway, since we have fewer sides, I can label the first set of index values for you.
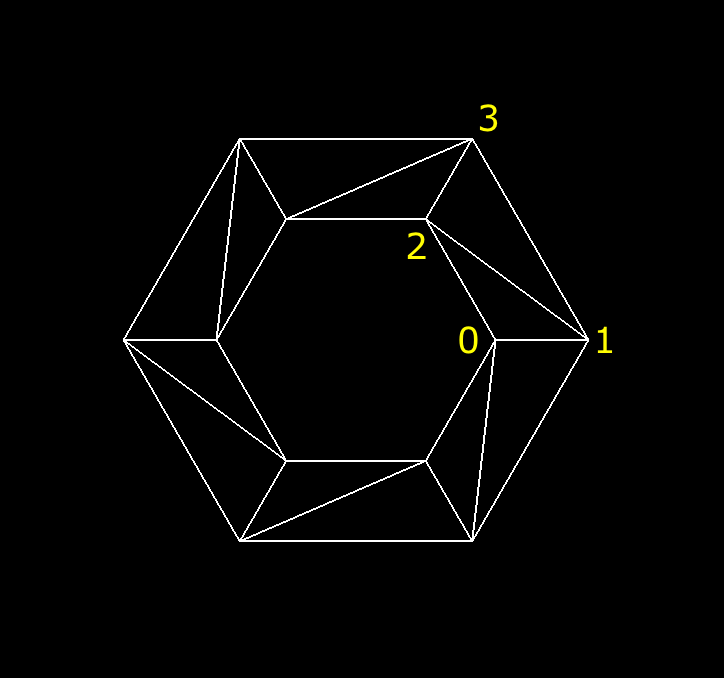
We do one iteration for each side of the donut. For each side, we calculate the indices of four of the points in our vertices array, and we build two Face3 triangles out of them. Put the two triangles together, and you get a trapezoid. Put all the trapezoids together, and you get a donut. Or at least an approximation of one. But for games, a close approximation is often as good as the real thing.
Donut Slices
Now it’s time to fill in those triangles! This looks like a job for uv mapping. You might be wondering why I chose a map of the Earth for our source texture. I wanted something you’d be familiar with, so you could see which portions of the texture are getting mapped to which areas around the mesh. If you scroll down again, you’ll find yourself at part // 6.
// 6
function getDonutFaceUvLayer(sidesCount) {
var faceUvLayer = [];
for (var sideIndex = 0; sideIndex < sidesCount; sideIndex++) {
var trailingProgress = sideIndex / sidesCount;
var leadingProgress = (sideIndex + 1) / sidesCount;
var trailingInnerUv = new THREE.Vector3(trailingProgress, 1.0, 0.0);
var trailingOuterUv = new THREE.Vector3(trailingProgress, 0.0, 0.0);
var leadingInnerUv = new THREE.Vector3(leadingProgress, 1.0, 0.0);
var leadingOuterUv = new THREE.Vector3(leadingProgress, 0.0, 0.0);
var trailingUvs = [
trailingInnerUv,
trailingOuterUv,
leadingInnerUv
];
faceUvLayer.push(trailingUvs);
var leadingUvs = [
trailingOuterUv,
leadingInnerUv,
leadingOuterUv
];
faceUvLayer.push(leadingUvs);
}
return faceUvLayer;
}
Take a minute to scrutinize that. At first glance, it’s almost identical to the function we just looked at to build the Face3s. But of course this time we’re setting up the parallel arrays of uv coordinates to map onto those Face3s. What’s actually going on here? Take a look at this exaggerated diagram that represents one iteration of our for loop.
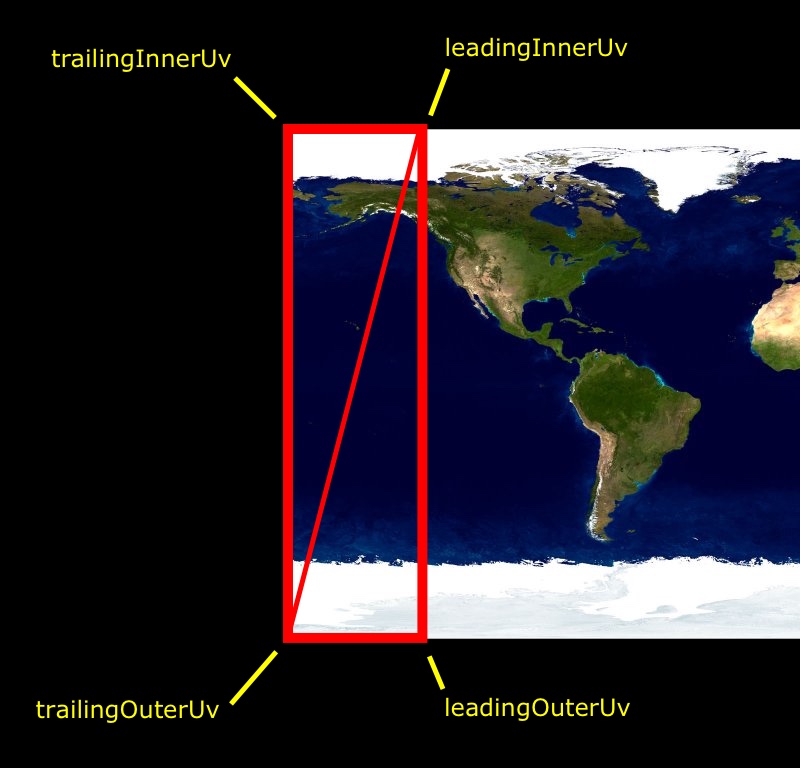
Here we’re constructing two triangles that fit together form a tall, skinny, rectangular slice of our texture. Every time we go through our for loop, we construct the coordinates for another rectangular slice and save them in our faceUvLayer array. We keep doing this until we’ve gone all the way across the texture. At that point, we have exactly the same number of rectangular slices as we have trapezoids that make up our donut approximation. When we render the donut, each rectangle will get mapped onto its own trapezoid. Pretty sweet, right?
Motivational Speech
That’s all the new code I have for you today. I hope you take the time to tamper with it on your own a bit. One interesting thing to try would be flipping the texture mapping over so that the South Pole is at the center of the donut. It’s actually just a matter of swapping some uv coordinates. And definitely see what other interesting mappings you can come up with as well. Nifty.
Thanks for reading! I hope that you’re beginning to feel confident with Meshes and mapping. They sound intimidating, but there’s really nothing overwhelming about them. It’s nothing more than associating values with vertices and interpolating between them. If you can wrap your head around the donut we just made, you can totally comprehend any other concept there is to learn in OpenGL. Hooray!
Your Downloadables
Click here to run the finished product!
And here’s a link to a downloadable version of the source code: silly_spiky_stars_and_donuts.html. Note that you’ll need to run it from inside the folder structure that we set up in the first tutorial, and you’ll also need the image we’re using in its own images subfolder.
